第四章
市場東エリア
草を何度もタッチ
円の直径を3等分して、1つの円の中に下の図のような3つの図形を作った。
ⅠとⅢの面積は等しいが、Ⅱの面積はどうだろう?
Ⅰよりも大きいだろうか、小さいだろうか?
円の面積は
「半径×半径×π(円周率)」
【解くイメージ】
円の中心を横にスパッと切って、下半分を横に反転させたものをイメージしてみよう。
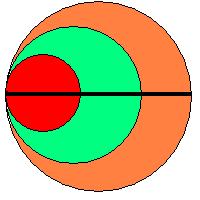
3つの円があり、それぞれの半径はの比率は「1:2:3」になる。
これを円の面積の公式に当てはめると、面積は「1:4:9」の比率になる。
小さい円の面積の半分を1として他の図形の面積を計算して見よう。